Base de Datos Orientada a Objetos
En una base de datos orientada a objetos, la información se representa mediante objetos como los presentes en la programación orientada a objetos. Cuando se integra las características de una base de datos con las de un lenguaje de programación orientado a objetos, el resultado es un sistema gestor de base de datos orientada a objetos (ODBMS, object database management system). Un ODBMS hace que los objetos de la base de datos aparezcan como objetos de un lenguaje de programación en uno o más lenguajes de programación a los que dé soporte. Un ODBMS extiende los lenguajes con datos persistentes de forma transparente, control de concurrencia, recuperación de datos, consultas asociativas y otras capacidades.
Las bases de datos orientadas a objetos se diseñan para trabajar bien en conjunción con lenguajes de programación orientados a objetos como Java, C#, Visual Basic.NET y C++. Los ODBMS usan exactamente el mismo modelo que estos lenguajes de programación.
Los ODBMS son una buena elección para aquellos sistemas que necesitan un buen rendimiento en la manipulación de tipos de dato complejos.
Los ODBMS proporcionan los costes de desarrollo más bajos y el mejor rendimiento cuando se usan objetos gracias a que almacenan objetos en disco y tienen una integración transparente con el programa escrito en un lenguaje de programación orientado a objetos, al almacenar exactamente el modelo de objeto usado a nivel aplicativo, lo que reduce los costes de desarrollo y mantenimiento.
Una base de datos es una colección de datos que puede constituirse de forma que sus contenidos puedan permitirse el encapsular, tramitarse y renovarse sencillamente, elementos de datos, sus características, atributos y el código que opera sobre ellos en elementos complejos llamados objetos. Las base de datos están constituida por objetos, que pueden ser de muy diversos tipos, y sobre los cuales se encuentran definidas unas operaciones donde interactúan y se integran con las de un lenguaje de programación orientado a objetos, es decir, que los componentes de la base de datos son objetos de los lenguajes de programación además que este tipo de base de datos están diseñadas para trabajar con lenguajes orientados a objetos también manipulan datos complejos de forma rápida y segura.
Las bases de datos orientadas a objetos se crearon para tratar de satisfacer las necesidades de estas nuevas aplicaciones. La orientación a objetos ofrece flexibilidad para manejar algunos de estos requisitos y no esta limitada por los tipos de datos y los lenguajes de consulta de los sistemas de bases de datos tradicionales.
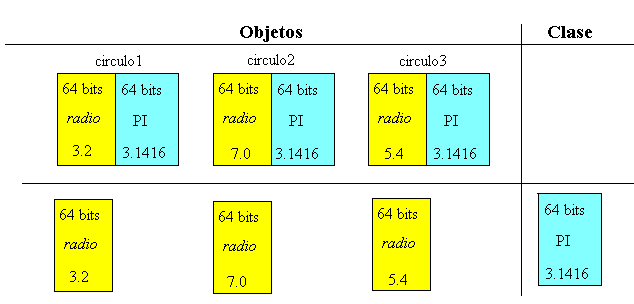
Los objetos estructurados se agrupan en clases. Las clases utilizadas en un determinado lenguaje de programación orientado a objetos son las mismas clases que serán utilizadas en una base de datos; de tal manera, que no es necesaria una transformación del modelo de objetos para ser utilizado. De forma contraria, el modelo relacional requiere abstraerse lo suficiente como para adaptar los objetos del mundo real a tablas. El conjunto de las clases se estructuran en subclases y superclases, los valores de los datos también son objetos.
Muchas organizaciones que actualmente usan tecnología orientada a objetos también desean los beneficios de los sistemas de gestión de base de datos orientados a objetos. En otras palabras, se desea la migración de bases de datos y aplicaciones de bases de datos relacionales a orientadas a objetos. La migración a la tecnología de objetos consiste de la ingeniería reversa de los programas de aplicación y la migración de la base de datos. El objetivo de la migración de la base de datos es tener un esquema equivalente y la base de datos disponibles. Esto desde luego puede ser logrado por medio de la transformación manual del código de los programas lo cual resulta demasiado complicado. Para esto existen tres enfoques que hacen uso de la tecnología de objetos para bases de datos relacionales.
a.- Construir una interface orientada a objetos sobre el sistema de base de datos relacional.
b.- La migración a un sistema de base de datos relacional/objetos.
c.- Conversión del esquema de base de datos relacional a uno orientado a objetos.
El primer enfoque retiene la base de datos relacional y crea una interface orientada a objetos encima de ésta. Este enfoque es el más fácil; no existe interrupción del sistema para la migración de datos y no existe perdida semántica de la información. Por otro lado el rendimiento disminuye debido que no existe un buen acoplamiento entre los dos paradigmas en el tiempo de ejecución.
En el segundo enfoque, los datos deben ser migrados de acuerdo con el motor de base de datos (por ejemplo Oracle 7 a 8), y las características orientadas a objetos solo pueden ser explotadas con la modificación o extensión del esquema.
El tercer enfoque es la migración de la base de datos en donde un nuevo esquema bajo el OODBMS es creado y los datos son migrados de la base de datos relacional a la orientada a objetos.
Una base orientada a objetos es una base de datos que incorpora todos los conceptos importantes del paradigma de objetos:
Encapsulación: Propiedad que permite ocultar información al resto de los objetos, impidiendo así accesos incorrectos o conflictos.
Herencia: Propiedad a través de la cual los objetos heredan comportamientos dentro de una jerarquía de clases.
Polimorfismo: Propiedad de una operación mediante la cual puede ser aplicada a distintos tipos de objetos.
En bases de datos orientadas a objetos, los usuarios pueden definir operaciones sobre los datos como parte de la definición de la base de datos. Una operación (llamada función) se especifica en dos partes. La interfaz (o signatura) de una operación incluye el nombre de la operación y los tipos de datos de sus argumentos (o parámetros). La implementación (o método) de la operación se especifica separadamente y puede modificarse sin afectar la interfaz. Los programas de aplicación de los usuarios pueden operar sobre los datos invocando a dichas operaciones a través de sus nombres y argumentos, sea cual sea la forma en la que se han implementado. Esto podría denominarse independencia entre programas y operaciones.
Origen de las base de datos orientadas a objetos
El origen se encuentra básicamente en las siguientes razones:
La existencia de problemas para representar cierta información y modelar ciertos aspectos del "mundo real", puesto que los modelos clásicos permiten representar gran cantidad de datos, pero las operaciones y representaciones que se pueden realizar sobre ellos son bastante simples.
El paso del modelo de objetos al modelo relacional genera dificultades que en el caso no surgen ya que el modelo es el mismo.Por lo tanto, las bases de datos orientadas a objetos surgen básicamente para tratar de paliar las deficiencias de los modelos anteriores y para proporcionar eficiencia y sencillez a las aplicaciones.
Las debilidades y limitaciones de los Sistema Gestor de Bases de Datos Orientadas a Objetos son:
Pobre representación de las entidades del "mundo real".
Sobrecarga y poca riqueza semánticas.
Soporte inadecuado para las restricciones de integridad y empresariales
Estructura de datos homogénea
Operaciones limitadas
Dificultades para gestionar las consultas recursivas
Desadaptación de impedancias
Problemas asociados a la concurrencia, cambios en los esquemas y el inadecuado acceso navegacional.
No ofrecen soporte para tipos definidos por el usuario (sólo dominios)
Mientras que las necesidades de las aplicaciones actuales con respecto a las bases de datos son:
Soporte para objetos complejos y datos multimedia
Identificadores únicos
Soporte a referencias e interrelaciones
Manipulación navegacional y de conjunto de registros
Jerarquías de objetos o tipos y herencia
Integración de los datos con sus procedimientos asociados
Modelos extensibles mediante tipos de datos definidos por el usuario
Gestión de versiones
Facilidades de evolución
Transacciones de larga duración
Interconexión e interoperabilidad
Debido a las limitaciones anteriormente expuestas, su uso es más ventajoso si se presenta en alguno de los siguientes escenarios:
Un gran número de tipos de datos diferentes
Un gran número de relaciones entre los objetos
Objetos con comportamientos complejos
Se puede encontrar este tipo de complejidad acerca de tipos de datos, relaciones entre objetos y comportamiento de los objetos principalmente en aplicaciones de ingeniería, manufacturación, simulaciones, automatización de oficina y en numerosos sistemas de información. No obstante, las BDOO no están restringidas a estas áreas. Ya que al ofrecer la misma funcionalidad que su precursoras relacionales, el resto de campos de aplicación tiene la posibilidad de aprovechar completamente la potencia que las BDOO ofrecen para modelar situaciones del mundo real.
Características
Una de las características mandatorias de o reglas son:
1.-Debe tener un motor de base de datos.
2.-Debe ser un sistema orientado a objetos.
Mandatorias.- Son las que el Sistema debe satisfacer a orden de tener un sistema de base de datos orientadas a objetos y estos son: Objetos complejos, Identidad de objetos, Encapsulación, Tipos ó Clases, Sobre paso combinado con unión retardada, Extensibilidad, Completación Computacional, Persistencia y Manejador de almacenamiento secundario, Concurrencia, Recuperación y Facilidad de Query.
Opcional.- Son las que pueden ser añadidas para hacer el sistema mejor pero que no son Mandatorias estas son de: herencia múltiple, chequeo de tipos e inferencia distribución y diseño de transacciones y versiones.
Abiertas.- Son los puntos donde el diseñador puede hacer un número de opciones y estas son el paradigma de la programación la representación del sistema ó el tipo de sistema y su uniformidad.
El modelo orientado a objetos se basa en encapsular código y datos en una única unidad, llamada objeto. El interfaz entre un objeto y el resto del sistema se define mediante un conjunto de mensajes. El término mensaje en un contexto orientado a objetos, no implica el uso de un mensaje físico en una red de computadoras, si no que se refiere al paso de solicitudes entre objetos sin tener en cuenta detalles específicos de implementación. El modelo de datos orientado a objetos es una extensión del paradigma de programación orientado a objetos. Los objetos entidad que se utilizan en los programas orientados a objetos son análogos a las entidades que se utilizan en las bases de datos orientadas a objetos puros, pero con una gran diferencia: los objetos del programa desaparecen cuando el programa termina su ejecución, mientras que los objetos de la base de datos permanecen. A esto se le denomina persistencia.
Ventajas e inconvenientes de las bas e de datos orientadas a objetos
Aunque los Sistema Gestor de Bases de Datos Orientadas a Objetos pueden proporcionar soluciones apropiadas para muchos tipos de aplicaciones avanzadas de bases de datos, también tienen sus desventajas.
Las ventajas de un Sistema Gestor de Bases de Datos Orientadas a Objetos son:
Mayor capacidad de modelado. El modelado de datos orientado a objetos permite modelar el "mundo real" de una manera mucho más fiel. Esto se debe a:
1. un objeto permite encapsular tanto un estado como un comportamiento
2. un objeto puede almacenar todas las relaciones que tenga con otros objetos
3. los objetos pueden agruparse para formar objetos complejos (herencia).
Ampliabilidad. Esto se debe a:
1. Se pueden construir nuevos tipos de datos a partir de los ya existentes.
2. Agrupación de propiedades comunes de diversas clases e incluirlas en una superclase, lo que reduce la redundancia.
3. Reusabilidad de clases, lo que repercute en una mayor facilidad de mantenimiento y un menor tiempo de desarrollo.
Lenguaje de consulta más expresivo. El acceso navegacional desde un objeto al siguiente es la forma más común de acceso a datos en un Sistema Gestor de Bases de Datos Orientadas a Objetos. Mientras que SQL utiliza el acceso asociativo. El acceso navegacional es más adecuado para gestionar operaciones como los despieces, consultas recursivas, etc.
Adecuación a las aplicaciones avanzadas de base de datos. Hay muchas áreas en las que los SGBD tradicionales no han tenido excesivo éxito como el CAD, CASE, OIS, sistemas multimedia, etc. en los que las capacidades de modelado de los Sistema Gestor de Bases de Datos Orientadas a Objetos han hecho que esos sistemas sí resulten efectivos para este tipo de aplicaciones.
Mayores prestaciones. Los Sistema Gestor de Bases de Datos Orientadas a Objetos proporcionan mejoras significativas de rendimiento con respecto a los Sistema Gestor de Bases de Datos Orientadas a Objetos relacionales. Aunque hay autores que han argumentado que los bancos de prueba usados están dirigidos a aplicaciones de ingeniería donde los Sistema Gestor de Bases de Datos Orientadas a Objetos son más adecuados. También está demostrado que los SGBDR tienen un rendimiento mejor que los Sistema Gestor de Bases de Datos Orientadas a Objetos en las aplicaciones tradicionales de bases de datos como el procesamiento de transacciones en línea (OLTP).
Los inconvenientes de un Sistema Gestor de Bases de Datos Orientadas a Objetos son:
Carencia de un modelo de datos universal. No hay ningún modelo de datos que esté universalmente aceptado para los SGBDOO y la mayoría de los modelos carecen una base teórica.
Carencia de experiencia. Todavía no se dispone del nivel de experiencia del que se dispone para los sistemas tradicionales.
Carencia de estándares. Existe una carencia de estándares general para los Sistema Gestor de Bases de Datos Orientadas a Objetos.
Competencia. Con respecto a los SGBDR y los SGBDOR. Estos productos tienen una experiencia de uso considerable. SQL es un estándar aprobado y ODBC es un estándar de facto. Además, el modelo relacional tiene una sólida base teórica y los productos relacionales disponen de muchas herramientas de soporte que sirven tanto para desarrolladores como para usuarios finales.
La optimización de consultas compromete la encapsulación. La optimización de consultas requiere una compresión de la implementación de los objetos, para poder acceder a la base de datos de manera eficiente. Sin embargo, esto compromete el concepto de encapsulación.
El modelo de objetos aún no tiene una teoría matemática coherente que le sirva de base.